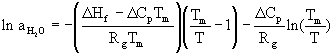Kristin N. Duvall, James A. Dirksen and Terry A. Ring‡

‡To whom correspondence should be directed.
 
 

Like any heat engine cycle, the Carnot efficiency (also called the "conversion factor" (1)) is given by difference in the high and low temperatures divided by the high temperature (1), h=(T_H-T_L/T_H). The combustion source heats the LiBr solution between 200 ºC and 250 ºC (473 to 523 K). To improve the Carnot efficiency and to better cool the building low temperatures are desired. But since the concentrated LiBr solution can freeze in the heat exchanger, plugging it if cooled to too low a temperature, this limits the efficiency of the adsorption heat pump. The freezing point of concentrated LiBr solutions depends upon their concentration since different solids (e.g. ice, tri-, di- and mono- hydrates of LiBr) are produced. To over compensate for this problem the heat pump is operated in a way such its low temperature is several degrees above the equilibrium freezing point of the concentrated LiBr solution. However, when cooled a concentrated LiBr solution, like all pure salt solutions, does not freeze at the equilibrium freezing point but at a temperature below the equilibrium freezing point due to the need to supersaturate the solution before nucleation can take place. This difference in temperature is called the Ostwald-Meyers meta-stable zone (2): its size depends on the type of solution. Little is known about the parameters that control the meta-stable zone but it should depend upon surfaces present, cooling rate, ...

The equilibrium freezing point of LiBr solutions is given as a series of fit equations, see Table 1, for various LiBr× nH₂O where n = 1, 2 and 3. This data is presented graphically in Figure 1 along with several experimentally measured equilibrium freezing points (3) found in the literature.

To establish the freezing point curve for ice, the water activity coefficient data by Patil et al. (4) were used and the equation (5)

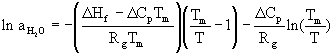[1]

where D H_f is the heat of fusion for water (+1,435.7 cal/mole), R_g is the gas constant, D C_p is the difference in heat capacity between ice and water (9.122 cal.mole^-1.° C^-1) at T_m, the normal freezing point of 273.15 K. The freezing point temperatures were calculated by inversion of the above formula for each water activity coefficient data point, which in turn was related to a particular solution concentration.

Figure 1 shows that the tri-hydrate, di-hydrate and mono-hydrate of lithium bromide have to be considered as the salt concentration increases. There are kinks in the solubility data which are indicative of a change in the solid phase crystallized. The liquid region is the region above the LiBr solubility curve and the equilibrium solubility of the ice curve. In addition, we also see a low temperature eutectic at a LiBr mass fraction of approximately 0.44 that freezes at » -25 ° C. This is the lowest temperature at which the LiBr solution should be liquid under equilibrium conditions. The solid crystallized at the eutectic is a mixture with about 56% ice and 44% LiBr•3H₂O using the lever rule.

The fit equations given in Table 1 can be reevaluated in terms of solubility products for each hydrated LiBr salt according to the equation:

[2]

where are the activity coefficients of the species in solution and are the mole fractions of species in solution. We can simplify this expression by using the Gibbs-Duhem equation,

 = 0 [3]

where X_i is the mole fraction of either LiBr or H₂O and g_{i is the activity coefficient of LiBr () or H2O (). Upon integration and substitution of , we find}

[4]

which can be then substituted into the solubility product, K_sp, giving

[5]

This expression for K_sp is only a function of the mean ion activity coefficient and the solution mole fraction of LiBr. Using the solubility fit equations, the values of the various solubility products for the mono, di and tri-hydrates are given in Table 2 along with their uncertainties.

[6]

where T₄₀ is the initial bath temperature, R is the slope of the set point ramp and C[=hA₀/m₀C_p0] is a grouping of parameters consisting of the bath heat transfer characteristics, h is the convective heat transfer coefficient for the refrigeration coils in the bath, A₀ is the bath heat transfer area, m₀ is the thermal mass of the bath and C_p0 is the heat capacity for this thermal mass. The cooling inside the test tube immersed in this bath undergoing ramped cooling follows the theoretical equation:

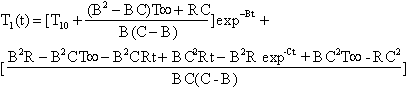[7]

where T₁₀ is the initial temperature of the fluid in the test tube, B [=U₀A/mC_p] is a group of parameters consisting of the test tube heat transfer characteristics, U₀ is the overall heat transfer coefficient for heat transfer from the bath to the LiBr solution in the test tubes, A is the heat transfer area, m is the thermal mass of the glass vial and the LiBr solution and C_p is the heat capacity for the entire thermal mass. Since the LiBr solution was soaked at 50 ° C for 24 hrs both T₁₀ and T₄₀ are the same temperature for these experiments. A plot of the set point, bath temperature and test tube temperature is given in Figure 2. To determine the values of C and B best fits of the bath temperature and the test tube temperature without freezing are performed as a function of time using equations 6 and 7. Excellent fits with errors less than 0.1 ° C are obtained.

Freezing is observed due to the deviation of the temperature from the theoretical value since the heat of crystallization for LiBr salts is large and exothermic. According to theoretic work by Lesoult (9), e.g. equation 7, the onset of nucleation is observed for small deviations from the theoretical cooling curve. With this experimental system deviations of 0.4 ° C are easily detected, see Figure 3. As the nucleation rate increases and the crystal growth rate increases, larger amounts of the heat of crystallization are released and the temperature of the LiBr solution increases against the cooling ramp. After the nucleation rate and the crystal growth rate slow, the temperature then decreases as the cooling ramp in the bath overcomes the release of the heat of crystallization. The minimum in the temperature is easily observed. Deviations of 0.4 ° C from the theoretical curve equation 7 are obtained with a more detailed analysis. The 0.4 ° C deviation is typically only 0.5 ° C above the minimum temperature, this is easily detected due to the slope change that occurs at the minimum.

When undissolved crystals are present in solution due to insufficient solubilization another freezing point is measured. An example of the cooling curve for a solution with and without undissolved seed crystals is given in Figure 5. The freezing points for the solution with and without seed are easily distinguished. The 0.4 ° C deviation temperature for the solutions with crystals present from a previous freezing experiment reproduced (± 0.5 ° C) the equilibrium freezing point data from Freier (3) plotted in Figure 4.

The freezing point data at ramp rates of 20 ° C/hr and 0.2 ° C/hr were also measured. The results are shown in Figure 6 and compared with the equilibrium data for the crystallization of LiBr·2H₂O and LiBr·3H₂O. As the cooling rate was decreased, a higher freezing point was measured corresponding to a thinner Ostwald-Meyers instability region. This is expected as the equilibrium freezing point theoretically occurs for an infinitely slow cooling rate.

Crystallization induction times were measured by ramping down the temperature from 50 ° C to a given temperature above the observed freezing point at a 20 ° C/hr rate. This temperature was held for 24 hours waiting for an increase in the temperature to be observed indicating the freezing of the solution. The average induction times and their error bars for these experiments are plotted in Figure 7 as a function of the plateau temperature for a 60.54 wt % LiBr solution. As the temperature increases from the metastable freezing temperature of 3.42 ° C toward the equilibrium freezing point of 11.8 ° C for this solution, the induction time also increases. As the induction time increases, an increase of the corresponding standard deviation is observed.

In all cases, the crystals formed are large plate-like shaped. Crystals were observed to form first on the bottom glass surface of the test tube, suggesting surface nucleation, instead of homogeneous nucleation, to be the important nucleation step in these experiments. When the solution was completely frozen, the crystal filled 50 to 80% of the test tube depending upon the solution concentration.

[8]

where D H_f is the heat of crystallization of the crystallizing solid, T is the actual temperature of crystallization, T_eq is the equilibrium crystallization temperature and R_g is the gas constant. The heat of crystallization of the crystallizing solid at various solution concentrations was obtained from the solubility data using

[9]

since the solubility fit equations are in a similar functional form, see Table 1. Using the experimentally observed freezing points, values of the critical supersaturation measured were typically, S_c » 1.1.

1) for homogeneous nucleation :

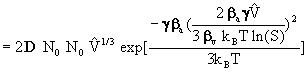[10]

and 2) for surface nucleation :

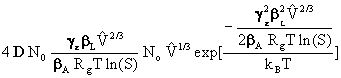= [11]

to determine a critical supersaturation that is responsible for these humanly observable nucleation rates. In the above equations, D is the solution diffusion coefficient, N_o is the number concentration of LiBr in solution, r^* is the critical radius for homogeneous nucleation (subscript s is for surface nucleation), g is the surface energy for the crystal/solution interface, g_?[»g_{d] is the edge energy per unit length, is the molar volume of the crystal.} b_{v and} b_{a are the volume and area conversion factors for homogeneous nucleation, (for spherical nucleii,} b_v=4p /3 and b_a=4p , for cubic nucleii, b_{v =1 and} b_a=6), b_{L is the edge length conversion factor and} b_{A is the surface area conversion factor for surface nucleation (for a cylindrical embryo of height, d/2, above the surface,} b_A= p and b_L=2p ; for cubic embryo with an effective radius = L/2, b_{A=1 and} b_{L=4), kB is Boltzmann's constant.}

_{The crystallization temperature was calculated by inverting equation 11 assuming that Is, the nucleation rate, equals 1 nucleus per cm² per minute. This freezing temperature is calculated assuming surface nucleation is responsible for spontaneous nucleation. The freezing temperature is highly dependent upon the value of the surface energy used for the foreign surface. A similar mathematical approach can be used for the freezing temperature assuming homogeneous nucleation is responsible for spontaneous nucleation.}

_{There are two unknown values in these classical nucleation rate equations (equations 10-11): 1) the diffusion coefficient, D, however, it must have a value approximately 10^-5 cm²/s for aqueous solutions, and 2) the surface energy of the crystal/solution interface,} g. All other terms have standard values assuming a cubic nucleus. The nucleation rates are linear dependent on the diffusion coefficient, D; non-linear dependent on the surface energy, g, and on the temperature, especially in the definition of S in equation [8]. The effect of either errors in the value of D, used in calculating the crystallization temperature, or in the constant nucleation rate of 1 nucleus/cm².min are smaller than the effect of errors in the crystallization temperature due to errors in the value of g. Thus the parameter g is the most critical parameter in determining the crystallization temperature using measurable nucleation rates.

The energy of the ice/water interface has been measured by Skapski et al. (10) to be 26 erg/cm². (Note the data point for freezing ultra-pure water at – 40 ° C (10) and fit with homogeneous nucleation curve in Figure 4.) Since the hydrated LiBr crystals will also have a layer of structured water at the surface, their surface energy is not likely to be very different from that of the ice/water interface. As a result this same value has been used for the surface energy of hydrated LiBr crystals undergoing homogeneous nucleation. The freezing point for an emulsion of concentrated LiBr solution in mineral oil measured by Dr. Austin Angel (12) is plotted in Figure 4 and is reasonably close to the homogeneous nucleation curve when one considers that errors in solution concentration can easily be made with this deliquescent salt. In an emulsion the solution droplets are more numerous than the dust particles present for heterogeneous nucleation to take place. For surface nucleation of hydrated LiBr salt at either the test tube surface or the thermowell surface, both made of pyrex glass, another interfacial energy should be used. This value was obtained from a best fit of the experimental freezing point data.

The experimental data points for our test tube experiments support the hypothesis that surface nucleation on the test tube surface is responsible for the nucleation event observed. For the surface nucleation curve, data points for a solution with 60.54 wt % LiBr was used to determine the appropriate value of the interfacial energy for surface nucleation. This freezing point corresponds to 3.42 ±  0.56 ° C, where the mean and standard deviation were determined with 69 separate freezing point measurements for this solution at a ramp rate of 20 ° C/hr. Assuming I_s to be one nucleus per cm² per minute the surface energy g was solved to give a value of 40.0±1.2 erg/cm². This value was then used for all other surface nucleation curves, showing good agreement with data for other concentrations where the di- and tri-hydrate crystallized from solution. The standard deviation of the surface energy was calculated by using the freezing point minus its standard deviation in equation [11] and solving for the surface energy.
 
 

With the slower cooling rates the freezing point increases, moving closer to the equilibrium freezing point as would be expected since the equilibrium freezing point is obtained by an infinitely slow cooling rate. Classical nucleation theory, which was shown to successfully predict the meta-stable freezing point as a function of concentration in Figure 4, does not predict the effect of cooling rate. As a result, an important phenomenon is missing in classical nucleation theory - the effect of cooling rate. It is suggested that further work on nucleation theory be done to incorporate the effect of cooling rate so that the meta-stable region can be calculated for different cooling rates.

The induction times measured can be compared to the induction time for homogeneous nucleation given by (13)

[12]

where n* is the number of molecules in the critical nucleus. This equation predicts that as S increases or the temperature is lowered below that of the freezing point, the value of the induction time decreases. A plot of this equation, not shown here, reveals the same shape, occurring at the same temperatures than the experimental data in Figure 7 but is four orders of magnitude lower. The reason for this discrepancy in crystallization induction times is probably due to limitations of classical nucleation theory, discussed above. The standard deviation of the crystallization induction time is also very large as shown in the error bars given in Figure 7. Since the induction time, t, depends upon the surface energy, g, we expect that heterogeneities in the surface energy lead to the large standard deviation in the induction time measured.

and the Molarity (in units of moles/Kg H₂O), M_LiBr, is given by :

where M_w is the molecular weight of either LiBr or H₂O.

G [], of the aggregates is a result of two terms, the free energy due to the new surface and the free energy due to the formation of new solid.

[1]

for cooling,
 
 

where v is the volume and a is the area of the aggregate, is the molar volume of the precipitate, Rg is the gas constant, g is the surface free energy per unit area and D  is the molar free energy for the phase transition [D  = -R_gT ln(S) or with cooling of the vapor ] where -D H_T is the enthalpy of the phase transition (either condensation for a gas or fusion for a melt) occurring at temperature T below the equilibrium temperature To. S [=a/a_o] is the saturation ratio, where a is the activity of the condensing species and ao is the activity in equilibrium with the condensate. A generalized particle radius, r (=3v/a), can be used to calculate the total free energy.

D G(r) = -(bv r³/ )R T ln(S)+ gba r², [2]

where bv is the volume conversion factor and ba is the surface area conversion factor. For a sphere, bv = 4p /3 and ba = 4p . For a cubic nuclei, bv = 8 and ba = 24. When the supersaturation, S<1.0, D G(r), is always positive and cluster formation is non spontaneous. When the supersaturation, S>1.0, D G(r) has a positive maximum at the critical size, r*, with a maximum Gibbs free energy, D Gmax = D G(r*). This is the energy barrier for nucleation. Clusters larger than the critical size will decrease their free energy by further growth, giving "stable nuclei" which grow to form macroscopic particles. Below the critical size, clusters will decrease their free energy by dissolving. The critical size, r*, is obtained by setting d /dr =0 giving

[3]

Nielsen (15) has adopted the terminology that an embryo is subcritical and a nucleus is supercritical in size. This critical size corresponds to a value of the free energy at the maximum of [4]

For a given value of S, all particles with r > r* will grow and all particles with r< r* will disappear. Embryo ConcentrationsUsing a Boltzmann distribution and these free-energy concepts, the equilibrium number density of embryos of size, r, is given byNe(r) = No exp[] = exp[] [5]

where N_o is number of molecules per unit volume of condensing material in the gas phase and k_B is Boltzmann's constant. This expression is only valid over a range of D G values where D G is greater than zero.Nucleation RateThe rate at which nuclei of critical size are assembled from an embryo and an additional atom is given by the reactionA(1 molecule) +B(r * - 1 molecule) ----> X(r *) [6]

which has the following rate assuming that only the forward reaction is considered :  [7]

where l_{AB is the rate constant for the collision between molecules (A) of concentration, No, with the units [] and nearly critical clusters (B) of concentration, []. Equation [7] is a simple result of the classical nucleation theory for the homogeneous nucleation rate with units of []. The collision rate constant for two different gas molecules is available from the kinetic theory of gases (16) :}[8]

where Mw is the molecular weight and s is the collision cross-section. The molecular weight correction term is rarely used in Classical Nucleation theory. Becker and Doring (13) give a more complicated expression for the collision rate as follows:l_{AB =} l_{AA()1/2 [9]}

_{Often the Gibbs free energy for a cluster of size, r*- 1 molecule, and for a critical cluster of size , r* are assumed to be the same, i.e.} D G(r*-1 molecule) »D G(r*) = D G_max. As a result, the Classical Nucleation rate is given by :

[10]

Classical Theory for MeltsTo alter Classical Nucleation rate theory to be valid in either solution or melts, the collision rate constant is altered in a way such as l_{AB = 2 D d or} l_{AB = exp[] [11]}

_{where D is the diffusion coefficient, d is the center to center distance when two molecules collide, i.e.} s_{AA =}p /4 d², for spheres and s_{AA = d² for cubes, kB is Boltzmann's constant, h is Plank's constant and} D G_D is the Gibbs Free energy for diffusion in the solution or melt. Also note that for a melt of one component No a d^-3.Finally, a useful concept is that of the critical supersaturation which is the value of S [=S_c] necessary to give a nucleation rate which is rapid on a basis humanly observable, say, 1 nuclei per cm³ per second (17).Surface Nucleation in a MeltWith surface nucleation, we have a collision between a diffusing molecule in the melt and a subcritical cluster attached to the surface. This collision rate will be different if the melt near the surface of the nuclei is stagnant or moving. If the melt is stagnant, molecular diffusion will transport the molecule to the surface. If the melt is moving, convective diffusion will transport the molecule to the surface. Let us assume that the surface is a disc of radius, R_d. When the melt is stagnant, the flux to a single subcritical surface cluster can be calculated by analogy to the current to an ultramicroelectrode (18) of radius, r :

j [ ] = 4 D N_o r [12]

where D is the diffusion coefficient. The radius of the ultramicroelectrode in the case of surface nucleation is analogous to the radius of the subcritical cluster attached to the surface of radius, r_s* - 1 molecule. Calculating the flux to all these subcritical clusters at the surface, the surface nucleation rate can be approximated by :

Is [] = 4 D N_o r_s* N_o d exp[] = l_{sD No No d exp[] [13]}

_{where the term No d exp[] is the surface concentration [] of critical nuclei of size rs* and} l_{sD [=4 D rs*] is the collision rate constant for diffusion. Note that the term Nod is the concentration of molecules at the surface. The above surface nucleation rate is not that typically used for surface nucleation but is faster than that given by the extension of classical nucleation theory to surfaces (19) :}

_{Is [] = D d No No d exp[] =} l_{sCL No No d exp[] [14]}

_{since each sub critical cluster has a highly curved diffusion profile and not a uniform diffusion profile as shown in Figures 1 and 2. At this juncture it is necessary to note that surface nucleation has a different definition of the Gibbs free energy from that for homogeneous nucleation,}

D Gs [] = - R_gT ln(S)+ g_?b_{L r [15]}

_where ge [»gd] is the edge energy per unit length. For a cylindrical embryo of height, d/2, off the surface, b_A= p and b_L=2p . For cubic embryo with an effective radius = L/2, b_{A=1 and} b_{L=4. When the supersaturation, S<1.0,} D G_s(r) is always positive and cluster formation is non-spontaneous. When the supersaturation, S>1.0, D G_s(r) has a positive maximum at the critical size, r_s *, with a maximum Gibbs free energy, D G_{s rmax} = D G(r_s *). This is again the energy barrier for nucleation.

 TABLES

TABLE 1 Solubility Fit Equations (20) for LiBr.nH₂O salts.
 

n	Fit Equation for Mole Fraction
1
2
3

 
 
 

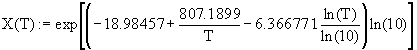TABLE 2 Solubility Products for LiBr•nH2O Salts.

These results assume that the mean ionic activity coefficient, g±, is 1.0.
 

Number of water molecules in Crystal, n	Ksp
1	0.042±0.005
2	0.020±0.002
3	0.010±0.001

 

List of figures
 
 

Figure 1 Freezing Points of LiBr solutions or LiBr Solubility [Mass fraction LiBr] as a function of temperature. The solid precipitating out of solution is different depending upon the temperature range of interest. The dihydrate is precipitated from 5.7 ° C to 34.6 ° C at 1 atm. pressure, the monohydrate above 34.6 ° C and the trihydrate below 5.7 ° C. Ice freezing identified at low LiBr concentrations. Some ice freezing point data (+) have been calculated from solvent activity coefficient data. For the LiBr•nH₂O solubility, theory (lines) and experiment (?) agree nicely.

Figure 2 Plot of the set point, T_s=trace 1, bath temperature, T_b=trace 2, and test tube temperature, T₁=trace 3 as a function of time.

Figure 3 Plot of experimental test tube temperatures when freezing is observed. T1b= bath temperature, T1m= measured test tube temperature, Tma, tma = maximum temperature and time, respectively; Tee, te = minimum temperature and time, respectively; Tc, tc = 0.4 ° C deviation temperature and time, respectively.

Figure 4 Equilibrium freezing point and crystallization temperatures versus weight fraction LiBr aqueous solution. Upper curves indicate equilibrium data for the crystallization of H2O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s). Middle curves indicate critical temperature, Tsc, (° C) for the surface nucleation of crystals of H2O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s) on glass surfaces. Bottom curves indicate critical temperature, Tc, (° C) for the homogeneous nucleation of crystals of H₂O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s). Experimental results for homogeneous nucleation of water gives –40 ° C (21) and 60 wt % LiBr solution (0.24 mole fraction) (in emulsion) gives –70 ° C (22) crystallization points. Other experimental data point come from present work. The average value of the freezing point is marked by the (+) symbol and the standard deviation is given by (?) symbols.

Figure 5 Cooling curve for a 61% LiBr solution with and without insoluble particles (of LiBr•2H₂O). In this case the temperature was lowered from 50 ° C to 30 ° C where it was held for 25 min. and then cooled at 20 ° C/hr to -10° C. This temperature plateau at 30 ° C was not used in subsequent experiments.

Figure 6 Equilibrium freezing point and crystallization temperatures versus weight fraction LiBr aqueous solution. Upper curves indicate equilibrium data for the crystallization of LiBr•3H₂O(s) and LiBr•2H₂O(s). Middle curve indicates the experimental freezing point due to cooling ramp at 0.2 ° C/hr and bottom curve indicates the experimental freezing point due to cooling ramp of 20 ° C/hr.

Figure 7 Induction time for 60.54 wt % LiBr solution at various temperatures slighty above the measured freezing point (3.42 ° C).
 
 
 
 

Figures

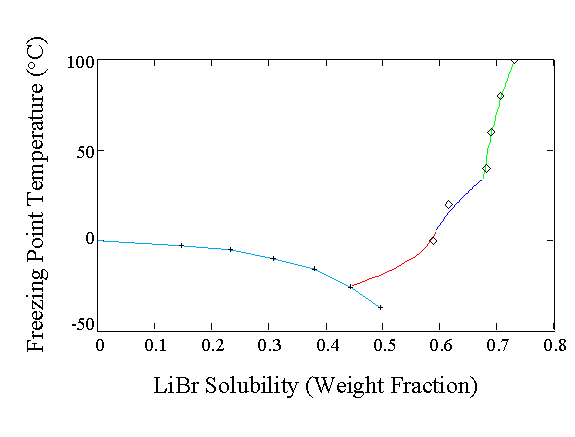
Figure 1 Freezing Points of LiBr solutions or LiBr Solubility [Mass fraction LiBr] as a function of temperature. The solid precipitating out of solution is different depending upon the temperature range of interest. The dihydrate is precipitated from 5.7 ° C to 34.6 ° C at 1 atm. pressure, the monohydrate above 34.6 ° C and the trihydrate below 5.7 ° C. Ice freezing identified at low LiBr concentrations. Some ice freezing point data (+) have been calculated from solvent activity coefficient data. For the LiBr•nH₂O solubility, theory (lines) and experiment (à ) agree nicely.
 
 

Figure 2 Plot of the set point, T_s, bath temperature, T_b, and test tube temperature, T₁ as a function of time.
 
 
 
 
 
 
 
 
 

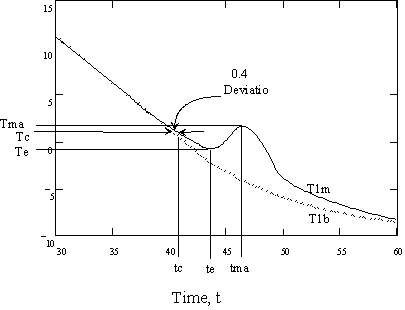F
 
 

igure 3 Plot of experimental test tube temperatures when freezing is observed. T1b= bath temperature, T1m= measured test tube temperature, Tma, tma = maximum temperature and time, respectively; Tee, te = minimum temperature and time, respectively; Tc, tc = 0.4 ° C deviation temperature and time, respectively.
 
 
 
 
 
 
 
 
 
 

Figure 4 Equilibrium freezing point and crystallization temperatures versus weight fraction LiBr aqueous solution. Upper curves indicate equilibrium data for the crystallization of H2O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s). Middle curves indicate critical temperature, Tsc (° C) for the surface nucleation of crystals of H2O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s) on glass surfaces. Bottom curves indicate critical temperature, Tc, (° C) for the homogeneous nucleation of crystals of H₂O(s), LiBr•3H₂O(s) and LiBr•2H₂O(s). Experimental results for homogeneous nucleation of water gives –40 ° C (21) and 60 wt % LiBr solution (0.24 mole fraction) (in emulsion) gives –70 ° C (22) crystallization points. Other experimental data point come from present work. The average value of the freezing point is marked by the (+) symbol and the standard deviation is given by (à ) symbols.
 
 
 
 
 
 
 
 

Figure 5 Cooling curve for a 61% LiBr solution with and without insoluble particles (of LiBr•2H₂O). In this case the temperature was lowered from 50 ° C to 30 ° C where it was held for 25 min. and then cooled at 20 ° C/hr to -10° C. This temperature plateau at 30 ° C was not used in subsequent experiments.
 
 
 
 

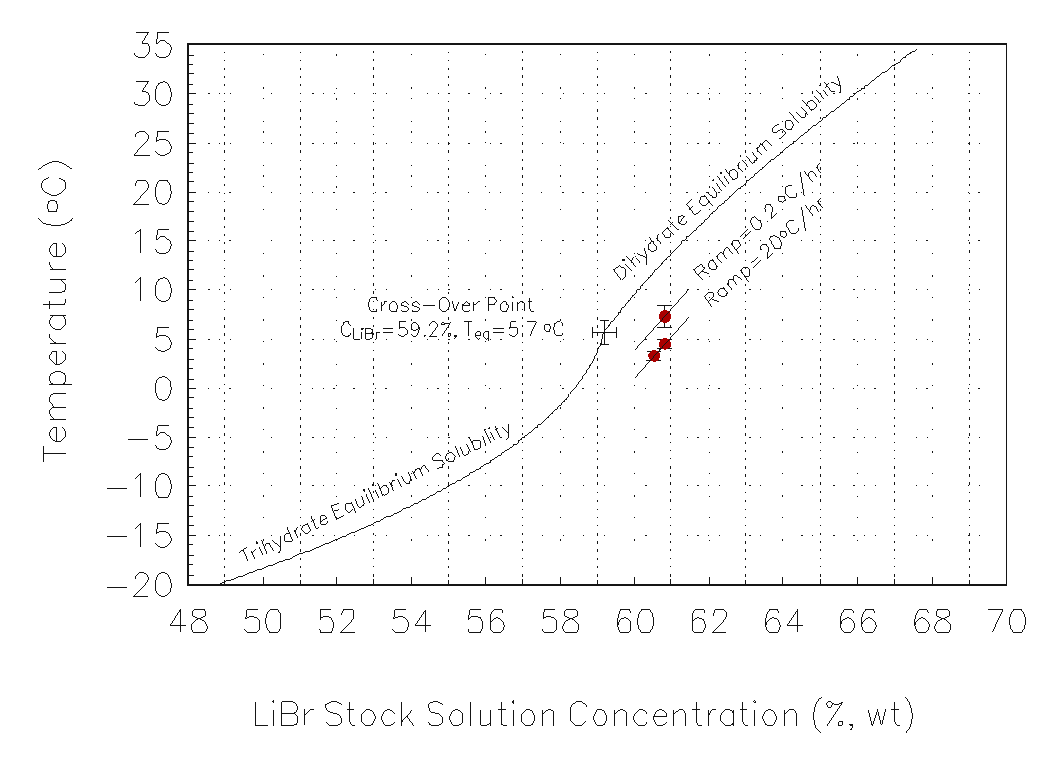
Figure 6 Equilibrium freezing point and crystallization temperatures versus weight fraction LiBr aqueous solution. Upper curves indicate equilibrium data for the crystallization of LiBr•3H₂O(s) and LiBr•2H₂O(s). Middle curve indicates the experimental freezing point due to cooling ramp at 0.2 ° C/hr and bottom curve indicates the experimental freezing point due to cooling ramp of 20 ° C/hr.
 
 
 
 
 
 

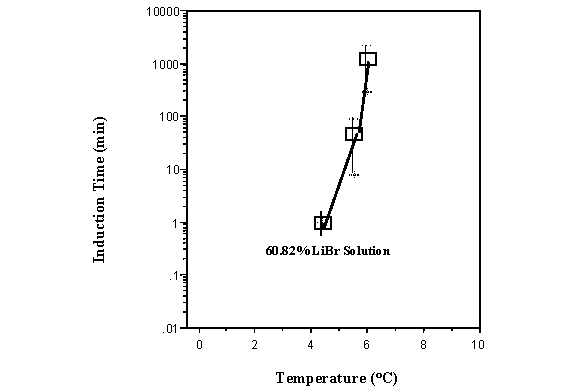
Figure 7 Induction time for 60.54 wt % LiBr solution at various temperatures slighty above the measured freezing point (3.42 ° C).