Ch En 4903-1
Example Problems
These problems are not part of the coursework and are only meant to give you practice with data analysis.
If you wish, you may complete these, hand them in to me, and I will check your work.
1. Your coworker tells you the temperature fluctuations of the outlet temperature from a certain coal gassifier have an average of 1304 K and keep within 12 K of that mean for 95% of her measurements, over months of operation. If we assume the temperature measurements are normally distributed, what is the standard deviation and what are the odds that a temperature measurement would be above 1310 K?
2. In a falling bead viscometer, the viscosity may be found by the following equation:
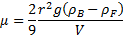
Where r is the bead radius, g is gravitational acceleration, V is the terminal velocity, rB is the bead density and rF is the fluid density. If we find, within a 95% confidence level, that the bead density is 2 ± 0.1 g/cm3, the radius is 3 ± 0.1 mm, the fluid density is 1.1 ± 0.2 g/cm3, and, after terminal velocity is achieved, the bead falls 10 ± 0.2 cm in 12 ± 0.5 seconds. What is the calculated viscosity and the uncertainty in its value? Which measurement is the greatest source of error?
3. You find the following particle size distributions from a spray dryer experiment:
| Size Range Minimum (mm) |
Size Range Maximum (mm) |
Particle Count |
0 |
0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 3.5000 4.0000 4.5000 5.0000 |
300 426 352 257 182 129 92 66 48 36 |
If we were to assume this distribution of particle sizes is log-normal, what would be the mean and standard deviation for the log-normal pdf?
4. On a certain stage of a distillation column theory predicts the ethanol concentration should be 27%. You take the following measurements over several runs:
| Percent Ethanol |
| 24.6 27.6 21.7 24.1 22.6 24.5 33.2 21.7 17.7 27.5 |
What is the likelihood that your measurements match theory?
5. You are measuring the effectiveness of a new catalyst on a reaction with a great deal of normally distributed variability. You measure the time to 99% conversion of your reactants with both your new and old catalyst for several experimental runs and find the following data:
| Old Catalyst (min) | New Catalyst (min) |
9.67 |
8.90
|
Given this data, what is the probability that the new catalyst is more effective than the old? What is the probability that they are equally effective?
6. The rate of population growth in a bacteria culture are found to be:
| Time (hr) | Rate of Population Growth (Some units that are reasonable but which I'm not going to figure out) |
| 0 0.3158 0.6316 0.9474 1.2632 1.5789 1.8947 2.2105 2.5263 2.8421 3.1579 3.4737 3.7895 4.1053 4.4211 4.7368 5.0526 5.3684 5.6842 6.0000 |
0.0078 0.2993 0.1895 0.3645 0.3097 0.2532 0.3469 0.3726 0.0260 -0.0107 -0.0246 -0.0623 -0.2936 -0.3387 -0.2570 -0.4667 -0.2095 -0.1778 -0.2522 -0.0271 |
It is thought that this data could be fit to the equation:
Rate=b1*sin(b2*t)
where b1 and b2 are constants to be determined and t is time. Determine the least squares estimated values for b1 and b2 and give an appropriate confidence interval for a confidence level of 90%. Also, what would you anticipate the rate to be at 24 hr? What would the confidence interval for a 95% confidence level be at 24 hr?