Error Propagation
|
Error Propagation Example:
Suppose you had a jar of honey and you wished to determine the viscosity of its contents, as well as the interval of our certainty in that value. Without more sophisticated equipment, a quick and simple way to do this would be falling sphere viscometry. In this experiment the terminal velocity of a bead falling through a viscous liquid is measured. Assuming stokes flow, the viscosity the fluid, μ, may be given by the following equation:
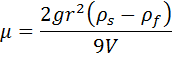
where r is the radius of the sphere, g is the gravitational constant, V is the terminal velocity, and ρs and ρf are the densities of the sphere in fluid, respectively.
From the perspective of error propagation, this equation brings several considerations to surface.
| f ( x1, x2, x3, x4, x5 ) = | f0 = ?? | |||||
| Continuous Method | Discrete Method | |||||
| i | xi | ei | df / dxi | ( df / dxi ei )2 | fi | ( fi - f0 )2 |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
Sum : |
||||||
Error, ef = (Sum1/2) : |
||||||