Descriptive Statistics
|
"It is known that there are an infinite number of worlds, simply because there is an infinite amount of space for them to be in. However, not every one of them is inhabited. Any finite number divided by infinity is as near nothing as makes no odds, so the average population of all the planets in the Universe can be said to be zero. From this it follows that the population of the whole Universe is also zero, and that any people you may meet from time to time are merely products of a deranged imagination."
~ Douglas Adams
One of the two main branches of applied statistics is known as descriptive statistics, which simply describe some numerical property of a set of data, with no indication on how that data relate to our hypotheses.
A measure of central tendency is meant to give us an indication of the most likely value in our data, or the point around which our data cluster.
Mean (1st Statistical Moment):
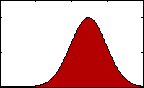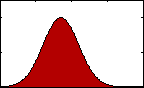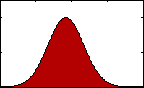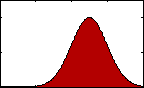 Figure 1: pdf with varying mean.
Figure 1: pdf with varying mean.The most familiar sort of descriptive statistics and most important measure of central tendency would likely be the mean, or average. A population's mean, μ, is found by summing all the data, xi, and dividing by the total number, N.
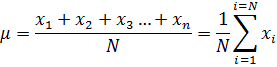
We may also calculate what is called a sample mean using only a subset of the population containing n values from the N possible (The difference between a population and sample statistical property is discussed in more detail and demonstrated below.). The sample mean is very similar to Equation (1):
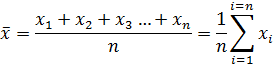
where n is the number of datum, xi, in the sample.
Interactive Example: If our data are , then the calculated sample mean would be ??.
The median value of a sample is the value, xmedian, which is less than (N - nmedian)/2 values of xi, and greater than the other (N - nmedian)/2 values, where nmedian is the number of values that equal the median value. Therefore, if we were to order our data from lowest to highest, the median would be the value in the middle of that list. If there is an even number of data points and thusly there is no single median value, the average of the two values closest to the middle is taken as the median.
Interactive Example: If our data are , then the calculated median would be ??.
The mode is defined as the most often occurring value in a data set. As such, there are often times when the mode is more than one number. For example, if our data are [4, 5, 5, 1, 3, 3, 5, 2, 3], then the data would be bimodal, with modes of 5 and 3. When the data are on a continuum and each value therefore is unique, there is no mode unless we round the data to some precision.
Interactive Example: If our data are , then the calculated median would be [??].
Measures of dispersion give us an indication of how broadly our data are spread out from their central tendency.
Standard Deviation (2nd Statistical Moment):
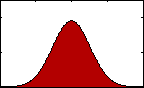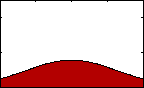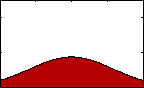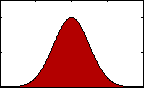 FIgure 2: pdf with varying standard deviation.
FIgure 2: pdf with varying standard deviation.The standard deviation gives us some idea of how broadly our data are spread out from their mean. Along with variance, this statistical property is among the most familiar and useful within the category of measures of dispersion. The standard deviation is defined as the square root of the average squared distance of each datum from the mean. As such, the population standard deviation is defined as:
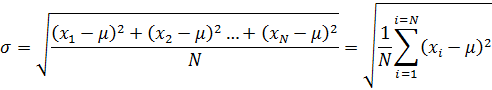
As with the mean, we may also find a sample standard deviation. Here, care must be taken, as the terminology becomes somewhat confusing. The following equation is for what we call the standard deviation of the sample:
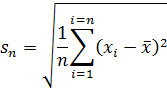
While Equation (5) is for the sample standard deviation:
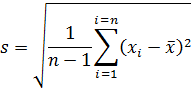
The difference between the two equations is in what is called the Bessel correction, using n-1 in place of n in Equation (4). This correction is most often used when calculating standard deviations, in order to correct for the fact that s is a biased estimator and tends to underestimate σ. Of course, as n becomes large, s will approach sn, but, as n approaches N, sn becomes the more accurate estimator of σ. These properties of the standard deviation and the reason for the Bessel correction are demonstrated in the section on population versus sample statistical properties, below.
Interactive Example: If our data are , then the standard deviation of the sample would be ??, and the sample standard deviation would be ??.
The variance is simply the standard deviation squared, which is the average squared distance of each datum from the mean. The population variance is therefore Equation 3 squared, and the sample variance is Equation 5 squared.
Interactive Example: If our data are , then the sample variance would be ??.
The range of data is the difference between the maximum and minimum values.
Interactive Example: If our data are , then the sample variance would be ??.
There exist several other descriptive statistical properties that may be useful in data analysis, aside from measures of central tendencies and dispersion.
Skewness (3nd Statistical Moment):
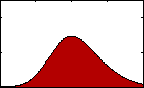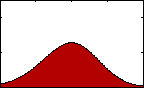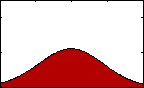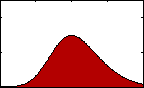 Figure 3: pdf with varying skew.
Figure 3: pdf with varying skew.Skewness gives us an indication of the asymmetry of our data. The equation for sample skewness is:
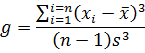
If the data are perfectly symmetrical about their mean, then g will equal 0, as it would for a normal or t-distribution. If g is negative, then the left tail of the distribution of our data is longer than the right. If it is positive, then the opposite is true.
Interactive Example: If our data are , then the skewness would be ??.
Kurtosis (4th Statistical Moment):
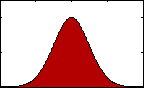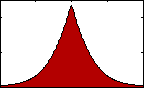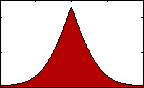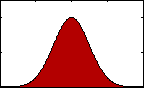 Figure 4: pdf with varying kurtosis.
Figure 4: pdf with varying kurtosis.Kurtosis is an indication of the pointedness of our data's distribution:
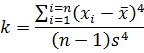
With a high k, most of the standard deviation is caused by extreme deviations from the mean. If k is small then most deviations are nearer the mean and the distribution is rounded.
For a normal distribution the kurtosis is 3 and sometimes excess kurtosis will be reported, which is simply k-3.
Interactive Example: If our data are , then the kurtosis would be ??.
Sample vs. Population Statistical Properties:
In statistics, we distinguish between properties of a sample and properties of an entire population. There are sample means and population means, sample standard deviations and a population standard deviations.
We make this distinction because most often we do not have access to the entire population of data. Nevertheless, we may wish to know some statistical property of that data. For example, say we wish to know the average maximum dimension of sand particles on a beach. To get that population's mean, we would have to measure every grain, an impossible task, and so we must settle for a sample mean. We would create a representative sample of the beach by picking a fraction of the total number of grains from random locations. We would then measure the maximum dimension of each grain in this small sample, and average those datum to find a sample mean, as an approximation of the population mean.
A demonstration of the difference between sample and population properties and the effect of sample size is demonstrated below. This applet creates a population of N normally distributed data points with a population mean of μ and standard deviation of σ. A plot of the entire population can be seen in the scatter plot.
|
|||||||||||
| Mean | Standard Deviation | ||||||||||
Once you press the "Begin Sampling" button, samples are randomly taken from the population. As each datum is chosen at random there is an incremental increase in the sample size, n (plotted on the x-axis on the Mean and Standard Deviation plots). For each sample size a sample mean (Equation 2), sample standard deviation (Equation 4), and standard deviation of the sample (Equation 5) is calculated and plotted. You may press the "Begin Sampling" button multiple times to see how results might vary for each experimental run.
As you can see, as the sample size increases, the sample mean more and more accurately estimates the population mean. See the section on confidence intervals and the Student T-Test for more information on how you may quantify the uncertainty in your sample means.
Note that with the sample standard deviation, we see a similar response to an increase in sample size, n. Also, it is apparent that the difference between the sample standard deviation (Equation 4) and standard deviation of the sample (Equation 5) is primarily important when the sample size is low (or when the population size is low and the sample size contains nearly the entire population). For example, decrease the population size to 15 and click the "Recreate Population Data" and then "Begin Sampling" several times. You should notice that, when n is small, the standard deviation of the sample most often underestimates the population standard deviation, while the sample standard deviation is closer to actuality. As is also apparent, if n is close to the value of N, then the standard deviation of the sample is closer to σ, but this is rarely the case; N is almost always unmanageably large.