University of Utah

Chemical Engineering Department

Test for Normalcy Projects Lab, University of Utah

 

" Every normal person, in fact, is only normal on the average."

 

~ Sigmund Freud

It is often in our research that we treat our data as though it were normally distributed, and the central limit theorem will often give us good reason. As such, our typical methods for propagating error and determining confidence intervals rely on such an assumption. Therefore, it is important to determine how reasonable an assumption of normality is.

• Q-Q Plot
• Skewness and Kurtosis
• Anderson-Darling Test
• Interactive Test for Normality Applet

Q-Q Plot:

The Quantile-Quantile Plot is means of visually determining how well our data fit a certain distribution. To construct a Q-Q Plot:

1. Sort the data, x, in increasing order to create a new vector, x_sort.
2. Calculate a percentage, P_i, for each sorted datum equal to the its order, i, in x_sort divided by the total number of data points, n.
3. For each P_i use the inverse CDF function for a normal distribution (or any other distribution of interest) to calculate a value, y_i.
4. Plot y_i verses x_sort.
5. It is typically useful to fit a line to the middle 60% of the data for comparison (most of the error will inevitably occur near the extreme values).

For an example of a Q-Q plot see the interactive applet at the end of this page.

 

Skewness and Kurtosis:

Skewness and kurtosis are the 3rd and 4th statistical moments and may be used to get a quick idea of your data's normality. The equation for skewness is described here, and kurtosis is described here. For normally distributed data, skew should be 0, as the data should be symmetrical about the mean, and kurtosis, a measure of pointedness, should be 3.

 

To see how kurtosis and skewness changes with various distributions see the interactive applet at the bottom of this page.

 

Anderson-Darling Test:

The Anderson-Darling test can quantify a confidence level in the hypothesis that our data are distributed normally. To perform this test:

1. Sort the data, x, in increasing order to create a new vector, x_sort.
2. Find the sample mean, m, and standard deviation, s.
3. For each sorted datum, calculate a value, y_i, as the normal CDF of x_sort with parameters of m and s.
4. Calculate an Anderson-Darling statistic:
   
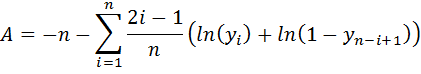
5. Correct for small sample sizes:
   
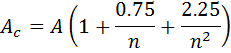
6. Calculate the percentage, P, as one minus the Anderson-Darling CDF of A_c. Typically these values are found in tables, as we have no analytical solution for the AD distribution. However, an approximation of the AD CDF can be calculated in and is plotted in the following applet:
   
   

   Anderson-Darling CDF

   x: f(x):

   c d f 1 0 0 2 x

   
    
7. If P is less than 5% then then hypothesis of normality is typically rejected.

To see how the Anderson-Darling test changes with various distributions see the interactive applet at the bottom of this page.

 

Interactive Test for Normality Applet

 

The following applet shows several tests for normality for data pasted into the text box below or synthetic data. A histogram for the data is plotted and a normal distribution is fitted to the histogram. In the last cell several of the tests for normality discussed above are implemented.

Enter or paste your data here (comma separated):	Or use synthetic data:
-3,-2,-2,-1,-1,-1,0,0,0,0,1,1,1,2,2,3	Mean norm StDev log-norm Number exp
Results:
Histogram Q-Q Plot for Normality   Hist. Bins: Number: 10 Mean:   StDv:   Conf.Level (measurement): % Conf Inv (measurement): Skewness:   Kurtosis:   ADstat:   Pr:  %

 

Take note how the Q-Q plot, kurtosis, skewness, and Anderson Darling probability change when you generate synthetic data with a log-normal or exponential distribution, verses the normal distribution.