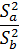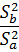Hypothesis Testing
2-(Treatments)
Projects Lab, University of Utah

 

"The best material model of a cat is another, or preferably the same, cat."

~ Norbert Wiener

Quite often we wish to compare two competing hypotheses. We typically call the hypothesis that our treatment has no effect on our data the null hypothesis, H0. This may be that our new drug is no better than our old drug or, say, that our data match the theoretical value. An alternative hypothesis, Hi, is an hypothesis that may be true if H0 is not. Such a hypothesis may be, for example, that our catalytic converter has fouled, or that our results do not agree with a theoretical prediction.

Steps in Testing a Hypothesis of Means:

  1. Determine the sample means, m, sample standard deviations, s, and the sample size, n, of data sets a and b. If comparing to theory, then data set b contains only a single value. Therefore, nb would be 1, mb would be equal to the theoretical value, and sb would be 0.
  2. Calculate the degrees of freedom, v.
     
     dof
     
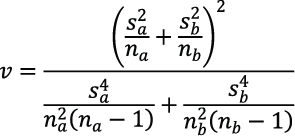
    Note how this equation simplifies if we are comparing to theory or if the sample sizes and/or standard deviations are equal.
  3. Calculate sab, the unbiased estimator of variance:

    sab

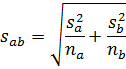
  4. Calculate the test statistic, t:

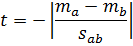
    tstat

  5. Calculate P using the values of t and v in the Student t-CDF:

    tcdf

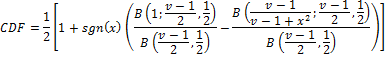
    where the beta functions in the numerators are incomplete beta functions and the denominators are beta functions. These values are typically found in tables or statistical software. The following applet, with t in place of x, may also be used to calculate the CDF value:

    Student-t CDF

    x:
    v:
    f(x):
    o
    c
    d
    f    		1
    0
    -55
    x

     
  6. Calculate the probability that your particular hypothesis is true, using a one tail or two tail test:
     
    H1
    H0
    Tails
    Eq. for Prob. That H1 is True
    μa ≠ μb
    μa = μb
    2
    1 - 2 * P
    μa > μb
    μa = μb
    1
    P if ma < mb and (1 - P) otherwise.
    μa < μb
    μa = μb
    1
    P if ma > mb and (1 - P) otherwise.

To see an graphical depiction of this process, and to perform a hypothesis test on your own data see the interactive applet, below.

 

Other sorts of tests:

It is important to note that many other sorts of hypothesis may be tested in a similar fashion. One simply needs to calculate the appropriate test statistic and use an appropriate CDF for calculating P. The following table shows a summary of frequently used tests on means and standard deviations.

UNDER CONSTRUCCTION,

THE FOLLOWING TABLE IS NOT FINISHED:

 

H0 Given Test Statistic CDF
μa ≠ μb Normally distributed data Case detailed above t
μa ≠ μb Normally distributed data
σa and σb are known		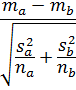 n normal
σa ≠ σb Normally distributed data

fa

 

fb

 F
σa ≠ σb

Normally distributed data

σb is known

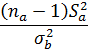 chi Chi2
       

 

 

These tests are shown for test data in the interactive below.

 

Interactive Hypothesis Testing Applet:

 

Data Set A: (comma separated) Data Set B: (or single, theoretical value)

Create Synthetic Data A
Mean
StDev
Number
Create Synthetic Data B
Mean
StDev
Number
Results:
Histogram Hypothesis Tests
 
Histogram Bins:
  Data A   Data B
Number: ?   ?
Mean: ?   ?
StDv: ?   ?
Skewness: ?   ?
Kurtosis: ?   ?
Std. Error: ?   ?
CL (meas.): %   %
CI (meas.):  
CL (mean): %   %
CI (mean):  
Pr(norm):  %    %
Hypothesis Tests on Means:
 StDv Unknown:
mA != mB mA > mB mA < mB
 StDv Unknown but Equal:
mA != mB mA > mB mA < mB
 StDv Known: StDv A = StDv B =
mA != mB mA > mB mA < mB
Hypothesis Tests on StDv:
 StDv Unknown:
sA != sB sA > sB sA < sB
 StDv B Known: StDv B =
sA != sB sA > sB sA < sB
Test Statistic ?
Degrees of Freedom ?
Probability of Hypothesis ?
Probability of Null-Hypothesis ?
bo