Statistics Visualization
|
"1001 words is worth more than a picture."
~ John McCarthy
Visualization of data is quite important in communicating and understanding statistical findings. The following introduction will discuss several common methods of presenting our data, and give an interactive example for each.
A dot diagram is one of the simpler means of displaying sets of data, and is primarily used to graphically display raw data. Data are plotted on a one dimensional axis, often with indications of some important descriptive statistical properties:
Interactive example (Might not "interact" in Firefox...):
|
Data A:
|
Dot Diagram for Data A Red = mean, Blue = Median, Yellow = ± one stdev |
|||||||||
Data B:
|
Dot Diagram for Data B Red = mean, Blue = Median, Yellow = ± one stdev |
|||||||||
Note that with a dot diagram you may be able to qualitatively compare two data sets by eye, and easily spot outliers in need of special consideration. With too many data points, however, the dots may overlap and conceal their distribution, making a scatter plot or a histogram more useful.
If you have too many datum to see clearly on a dot diagram where the bulk of your raw data exist, or how it is distributed, you might opt for a scatter plot. In this case, your data is plotted in the y-axis with an arbitrary data index number in the x-axis.
Interactive example:
| Data: |
A scatter plot is also useful in visually determining if data are correlated. For example, for each reactor run you may measure yield and reactor temperature. By plotting each data point on a scatter plot, with temperature on the x-axis and yield on the y-axis, a correlation may be observed in the grouping of dots along some axis.
Interactive example:
Data A:
|
|
Data B:
Generate Synthetic Data B:
|
A histogram is a commonly used and quite useful means of displaying data, due to its relationship to the data's probability distribution function (pdf). In a histogram, the 1-D axis of possible values of data is segmented into bins of some set width. These bins typically span a range equaling the total range of the data divided by the number of desired bins. Each bin is then given a number equal to the total number of data points that fall into the bin's range. These totals are then plotted as a bar graph, with each bar spanning from its bin's minima to its maxima, and its height equal to the number of data points that fall in that range.
A histogram, with a proper number of bins and properly normalized, should closely follow the pdf of the data. Thus the histogram may be used to, for example, visually determine if your data significantly deviate from a normal distribution.
In the following example a histogram is created from the data in the Dot Diagram example above. Along with the histogram, an indication of the mean and standard deviation is given at the top of the graph, along with a fit of a normal distribution pdf.
Interactive example:
Histogram:
|
|||||||||||||
Data A:
|
Dot Diagram for Data A Red = mean, Blue = Median, Yellow = ± one stdev |
||||||||||||
Data B:
|
Dot Diagram for Data B Red = mean, Blue = Median, Yellow = ± one stdev |
||||||||||||
Note that you can see, by comparison with the dot diagrams, how each data point contributes to the height of each bar in the histogram. You may create new data by altering the number of data points, n, the mean, m, or the standard deviation, s, below the data window for Data A or B.
You should notice that there is a balance to be found in choosing the number of bins, Nbins. With too few bins or too many bins, details of the data's distribution is lost. You may alter the number of bins and the number of data points in the above example to get a feel for this tradeoff.
There are several suggested methods for determining bin size (some of which may be implemented in the above example):
Square-Root:
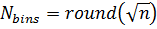
Sturges' Formula:
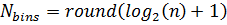
Scott's Choice:
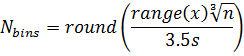
Freedman-Diaconis' Choice:
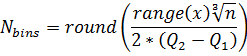
While such equations are useful starting points, each new histogram may benefit from some trial and error to find the optimal, most visually informative number of bins.
Probability Distribution Function (PDF):
Given enough data points, a histogram will eventually form the rough shape of the probability density function governing the random error behind our data. Similar to a histogram, on the x-axis of a pdf plot are the values that a random variable (such as our physical measurements) might take. If, for example, we were measuring the pH of ocean water samples, the pdf plot of that measurement would have pH on the x-axis. Unlike a histogram, though, in the y-axis is the relative likelihood that a certain measurement might occur. See this page for a detailed description of pdf's and examples of their graphical depictions.